Learning Rust - SlothDB
I’m learning Rust and looking for fun things to implement along the way. Something that I’ve been interested in doing for a while is writing a key-value store backed by an LSM tree, so that’s what I did! This post dives into the first version of what I’m calling SlothDB. I’m going to caveat this with the fact that SlothDB was always meant to be throwaway:
- I’m early enough in the process of learning Rust that the code I wrote at the beginning of the project was likely to end up much worse than the code I would write at the end.
- I enjoy learning by struggling through things myself. It’s a great way to get a feel for how things work, but does mean that I don’t get to leverage other peoples’ learnings, which are useful for actually building good software.
As such, my plan was to implement a quick-and-dirty first version to more deeply understand LSM trees and then scrap it and write a more “standard”2 implementation.
What are LSM trees?
Before we look at SlothDB, it’ll be useful to understand the data structure that backs it: an LSM tree. LSM trees are a data structures that underlie many modern key-value data stores and are optimized for high write throughput. That high write throughput is achieved through a multi-tiered approach to data storage where data is immediately stored in memory on write (which is fast) and flushed to disk in batches. When reading the value for a given key, the DB first checks the data store in-memory; if the key’s not present there, the DB uses indexes to find and read the value from disk efficiently.
A real database implemented on an LSM tree (and many of the examples of LSM trees you’ll find online) will have many moving parts3, but the core components are:
- A way to store data in memory temporarily
- A way to flush that data to (immutable) tables on disk with some indexing strategy that makes retrieving it sane
- A way to merge those tables on disk to avoid the database exploding in size as more writes occur
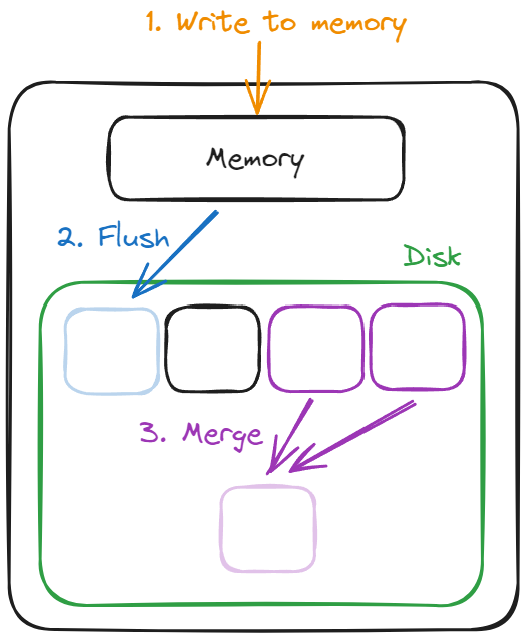
Let’s take a look at each of those steps in a little more detail.
1. Write to memory
When a value is written to an LSM tree, its stored in memory as a key-value pair, so if a request comes in for that key while it’s still there, it’s served straight from memory. Once that in-memory storage reaches some predetermined threshold, however, it’s flushed to disk.
2. Flush
The flushing process writes the in-memory data as a Sorted String Table (SSTable). SSTables are sorted by key and have corresponding indexes that make retrieval by key efficient. The SSTables in an LSM tree are immutable; once they’re written, they stay in the same state until they’re deleted. As a result, if a new write arrives on the DB for a key that’s already been flushed to disk (as with user1 in the example below), the DB can end up with two SSTables containing values for the same key:
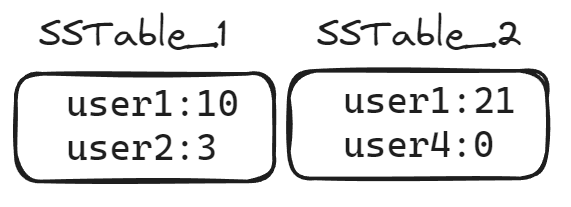
Since the latest value for a key is always the “real” one, the DB can find the current value for a key by starting from the newest table and scanning backwards in time to find the first one that contains a value for it. Some implementations use an index or bloom filter4 to keep that scan efficient. If the DB doesn’t find the key by the time it reaches the last table, then no value exists for the key. When a key is deleted, a special tombstone value is written for the key, which sets the latest value for the key to “deleted”:

Merge
If we did nothing else, the database would work, but it would keep growing forever as more data is written and more tables are flushed to disk. From the previous step, we know that multiple tables could contain values for the same key. We can use that to our advantage and merge tables together while throwing away duplicate (stale) data; because SSTables are sorted, the plain old efficient merge algorithm works well here. If we merged SSTable_1 and SSTable_2 from our earlier example, we could throw away the old value for user1 as we merge the two:
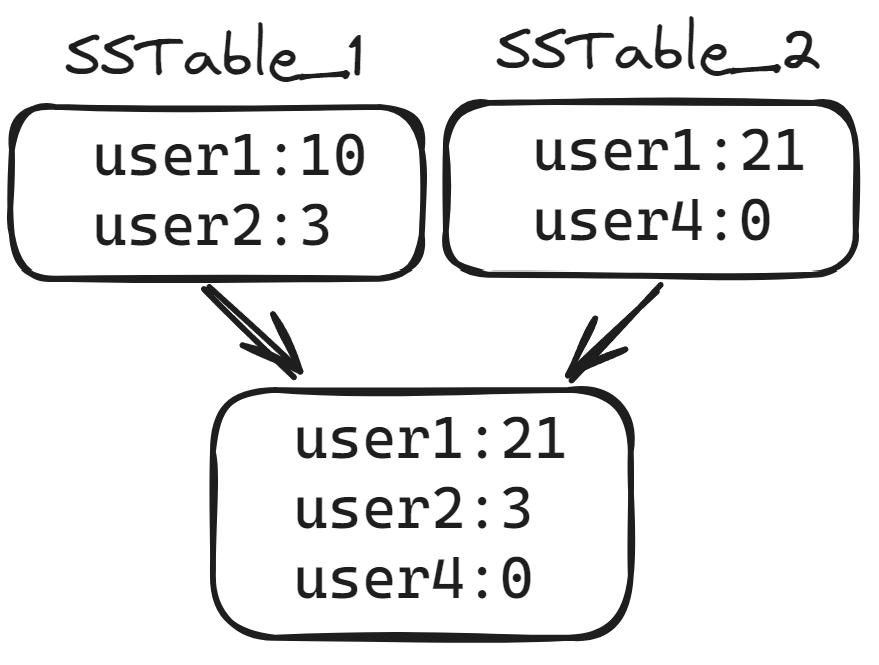
Specifically how an LSM manages tables before, during, and after merging depends on the LSM in use.
SlothDB - Possibly the slowest KV store in existence
Now that we’ve covered the important bits of an LSM, we can take a look at how SlothDB works. There’s a bit too much code to walk through all of it in a blog post of reasonable length, so I’ll just touch on the more interesting bits. As always, the code’s readily available for you to judge so go wild.
SSTables
Let’s start from the bottom and work our way up from SlothDB’s SSTables.
Structure
The SSTables each consist of two parts: an index file (with a .index extension) and a data file (with a .data) extension. The index files consist of newline-separated keys and the corresponding character offset and length of the keys’ data in the data file. The data files then consist of the concatenation of the values for all keys in the table5.
Let’s take this set of key-value pairs as an example:
bar:someValue
baz:anotherValue
egg:thirdVal
foo:helloWorld
Flushing them to disk would result in an index file that looks like:
bar:0,9
baz:9,9
egg:18,7
foo:25,9
and a data file that looks like:
someValueanotherOnethirdValhelloWorld
Flushing to disk
The flushing logic is fairly straightforward. The flush method takes the name of a table and writes the (assumed to be sorted) data from an iterator to the index and data files:
pub fn flush<'a>(file_name: &str, in_data: impl IntoIterator<Item = KV>) -> Result<(), TableErr> {
let mut out_data: Vec<String> = Vec::new();
let mut out_index: Vec<String> = Vec::new();
let mut position = 0;
for datum in in_data {
out_index.push(format!("{}:{},{}", datum.key, position, datum.value.len()));
out_data.push(datum.value.clone());
position = position + datum.value.len();
}
// Snip actally writing to disk
}
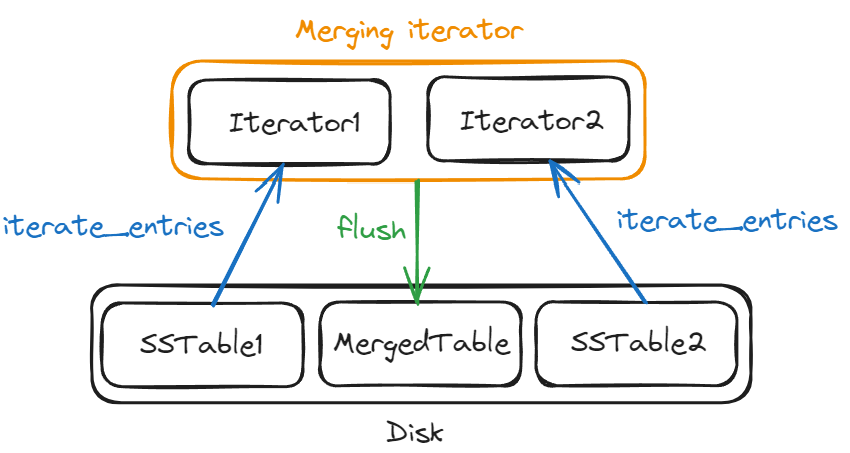
What I found fun was that creating an iterate_entries function (which produces an iterator over the entries in a file) let me write a merging iterator (that merges two sorted iterators on the fly) and pass it straight to flush:
pub fn merge_and_flush(left_file_name: &str, right_file_name: &str, new_file_name: &str) -> Result<(), TableErr> {
// Grab iterators for the two files to be merged
let left_iter = iterate_entries(left_file_name)?;
let right_iter = iterate_entries(right_file_name)?;
// Build a merging iterator over the two files
let merge_iter = MergeIter::new(left_iter, right_iter, |left_result, right_result| {
// Snip some details around merging
});
// Pass the merging iterator to flush
let _ = flush(new_file_name, merge_iter);
Ok(())
}
Here’s a nice picture of the process:
The LSM structs
flush and its friends handle writing to disk well enough, but it needs to be pointed at specific files, so I also needed some logic to manage the tables on disk and coordinate their compaction. The LSM tree consists of multiple levels, each with its own max capacity. When a level becomes full (or is over-filled), the two oldest tables in the level are compacted and pushed to a “lower” level. If that causes the lower level to become full, it’s compacted too. That process continues until every level is no longer full:
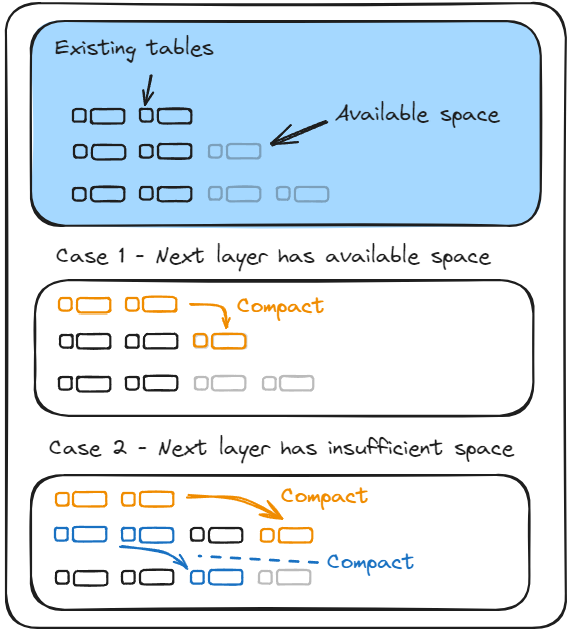
I implemented LsmTree and LsmLevel structs to model the data structure in memory, but the interesting part of their implementation is the LsmTree::compact function, since it’s the one that models the behaviour I described above. It uses LsmLevel::oldest to get the two oldest tables in the current level and passes them to the merge_and_flush method from earlier to compact them into a new table.
impl LsmTree {
fn compact(&mut self) -> Result<(), TableErr> {
for level_index in 0..self.levels.len() {
// A lower level can only become full if a level above it
// undergoes compaction, so break out as soon as a level
// isn't full.
if !self.levels[level_index].full() {
return Ok(());
}
// We need another level
if level_index + 1 >= self.levels.len() {
self.add_level();
}
let compaction_candidates = self.levels[level_index].oldest()
.expect("Couldn't pull oldest from the old level");
let destination = self.levels[level_index + 1].new_table();
let _ = table::merge_and_flush(
&compaction_candidates.0,
&compaction_candidates.1,
&destination)?;
let _ = table::clean(&compaction_candidates.0)?;
let _ = table::clean(&compaction_candidates.1)?;
};
Ok(())
}
// ... More functions
}
There are a few notable behaviours here:
- I don’t limit the size of each table. The compaction of two tables will always result in a single table, even if it’s much larger than the tables it was built from.
- There’s no locking at all. SlothDB is currently single-threaded and has no concurrency at all. In a real DB that cared about performance, compaction wouldn’t happen as part of a write request, so there’d need to be background threads that take a lock when they swap in the new table and remove the old ones.
Reading from the tree
When you read the value for a key from the LsmTree, it scans each of its LsmLevels top-down to try find the requested key. Those calls to each LsmLevel cause them to scan through their tables newest-to-oldest for the first one that contains the key. The first value that’s encountered for a key is the latest one and is immediately returned.
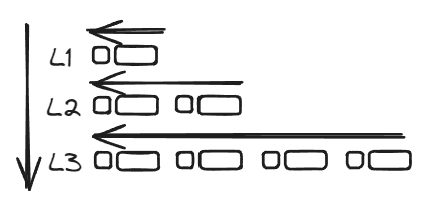
The in-memory component
I felt like implementing a binary search in Rust, so my in-memory component stores a sorted list of key/value pairs and uses a binary search to retrieve values by key. Any reads that don’t find a value in memory are deferred down to the LsmTree. Once the in-memory list reaches its maximum size, it flushes to the LsmTree and kicks off all of the behaviours I described earlier.
Closing out
Now that I’ve had a chance to get a little more familiar with LSM Trees and Rust, my plan is to throw away of SlothDB’s current implementation and start again. The second version of the DB will actually have some thought put into performance and should be much faster as a result. Look out for a future blog post on that!
Footnotes
-
DALL-E prompt: “Make a cartoony drawing of an LSM tree storing several key value pairs” ↩
-
Read: “good” ↩
-
Once I rewrite SlothDB to not be slower than a KV store powered by a mechanical turk, I’ll write another post about some of those improvements. ↩
-
I wrote about bloom filters in an earlier blog post. ↩
-
Using a binary encoding for the files on disk would’ve helped improve performance, but this representation made it really easy to see what was going on while I was still learning. ↩